Photo by Melissa Waterman
The Damariscotta artist Jacques Vesery creates elegant wooden bowls, cups, and sculptures carved in repetitive patterns of leaves, feathers, and other natural shapes. I happened to hear Vesery at a gallery one evening explain to a slightly puzzled patron his interest in the Fibonacci sequence of numbers and its relation to nature. Always an avid eavesdropper, I registered the term in my head, then looked it up the next day. Before I knew it, I was seeing Fibonacci sequences in empty whelk shells and sea-washed peach pits along the shore, in the pine cones that litter my lawn and in the tree’s branches themselves. Thus I have to conclude: The world around us, folks, is a mathematical construct!
Once upon a time there was a inquisitive Italian from Pisa who, around 1202, published a book in which he noted a curious mathematical sequence: 1,2, 3, 5, 8, 13, 21, 34, 55, 89 . . . . Leonardo Pisano, known as Fibonacci, pointed out that each number, except one, is the sum of the preceding two numbers. “Terrific,” said the world, which about that time was busy contemplating the Black Death and getting ready for the Inquisition. “So what?”
It turns out that the ratio between each number in the Fibonacci sequence is very close to 1.62, that is, 8 is about 1.62 times larger than 5 (actually, the higher in the sequence you go, the closer the ratio is to 1.62). This ratio is also what the Greeks referred to in ancient times as “the golden mean.” The Greeks used the golden mean in art and architecture and considered it to be a divinely set ratio. Only those human constructs that drew upon that ratio were considered “beautiful” to the discerning Greeks. They expressed the 1.62 ratio in the dimensions of their temples, where the longer sides of the building were approximately 1.62 times the length of the shorter sides. The height of the columns supporting the temples are in a golden mean proportion to the length of the pediment.
Then, in the seventeenth century, a mathematician named Jakob Bernoulli discovered that the proportions expressed in the golden mean could be found not only in Greek architecture but also in the natural world. Bernoulli drew a rectangle, with the long sides 1.62 times longer than the shorter. He then divided that rectangle to form a square and a rectangle. Bernoulli continued dividing the resulting rectangles into a square and a rectangle. When he bisected each square with a connecting center-line, he found that he had shaped a rough spiral.
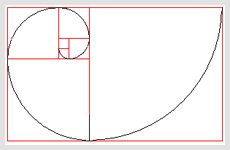
Bernoulli’s spiral
Taa dah! Each part of Bernoulli’s spiral turns out to be 1.62 times larger than the preceding segment. Bernoulli was so taken with this figure, known as the logarithmic or equiangular spiral, that he had it carved on his gravestone prior to his death.
Bernoulli’s spirals are everywhere in nature, appearing so frequently that some deep thinkers wonder if they could possibly be due to chance. On the head of a ripe sunflower are spirals of sunflower seeds spinning outward in a classic Fibonacci sequence The face of Queen Anne’s lace is composed of tiny spirals of minute flowers. That heavy whelk shell I found at the beach curves round and round itself in a clear spiral. Of course, the most famous spiral found in the ocean may be that of the chambered nautilus. The chambered nautilus is a mollusk that constructs internal airtight chambers to give itself buoyancy. When it outgrows its first chamber, it creates the next in a progressive curve which – you guessed it – is an equiangular spiral with a 1.62 ratio.

Even the lowly sunflower adheres to the spiral principle.
Photo courtesy Windsor Street Design, Rockland.
To be frank, I’ve never been particularly fond of numbers. Most mathematical equations cause me to break out in a peculiar sweat. Yet the peculiar reoccurance of this number derived from a simple numerical sequence tickles my curiosity. Plus it seems that as a human being (the ratio of whose hand to forearm length is – surprise! – 1.62), I respond intuitively to that ratio when I see it around me.
Philosophers have long considered the Greeks’ Golden Mean to reflect a divine symmetry intrinsically appealing to human eyes. When viewing the beauty of the swirls in a sunflower’s face or the delicate spiral of a seashell, I find myself surrounded by the mystery of mathematics.
 Photo by Melissa Waterman
Photo by Melissa Waterman Bernoulli’s spiral
Bernoulli’s spiral Even the lowly sunflower adheres to the spiral principle.
Even the lowly sunflower adheres to the spiral principle.
 Photo by Melissa Waterman
Photo by Melissa Waterman Bernoulli’s spiral
Bernoulli’s spiral Even the lowly sunflower adheres to the spiral principle.
Even the lowly sunflower adheres to the spiral principle.